Fundamental Theorem of Linear Programming
Published:
Fundamental Theorem of Linear Programming Given a linear program in standard form where A is an m × n matrix of rank m,
- (T1) if there is a feasible solution, there is a basic feasible solution;
- (T2) if there is an optimal feasible solution, there is an optimal basic feasible solution.
Feasible and basic solution
Corresponding to a linear program in standard form
\[\begin{align} \min c^Tx \\ \text{s.t. } Ax = b, x\ge0 \end{align}\]a feasible solution to the constraints that achieves the minimum value of the objective function subject to those constraints is said to be an optimal feasible solution. If this solution is basic, it is an optimal basic feasible solution.
Definition
\[\begin{align} A_s:= &\{x | Ax=b \}, &\text{affine subspace}, \\ O:= &\{x | x_i > 0 \}, &\text{orthant} \\ F:= & A_s \cap O, & \text{Feasible solution} \\ D:= & \{x | \lVert x \rVert_0 \le m, x \in R_n \}, & \text{m-sparse set: BASIC} \end{align}\]Then, (i) means, if
\[F \neq \emptyset\]then
\[F \cup D \neq \emptyset\]Geometry
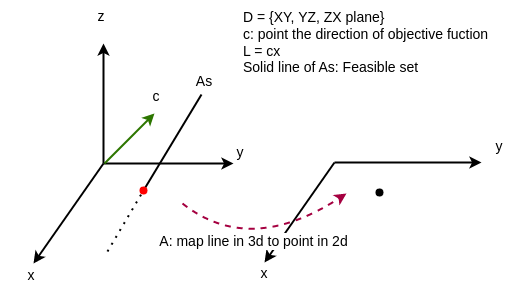
first part of the theorem (T1)
As you can see above, let A be a 2 x 3 matrix with rank 2, Ax=b define a line (affine subspace), then the first part of the theorem says that, is As has some part falls in the orthant (x, y, z >= 0), then line As must intercept planes of XY YZ ZX. The red dot above is an interception point and a basic feasible solution
second part of the theorem (T1)
F is As cut by orthant D, F is convex. And the boundary facets of F must lie in D, so that \(c^T x\) must reach a basic minimum.
This is an interpretation in 3D, in high dimensional space the author does not understand.
Another proof of T2
if z minimize \(c^T x \) in feasible set F and the minimum is \(l\), we can form
\[\begin{bmatrix} A\\ c^T \end{bmatrix} x = \begin{bmatrix} b\\ l \end{bmatrix}\]then T2 follows from T1, naturally
see
- Linear and Nonlinear Programming - Luenberger 2021 5th. Page 26
